1. Uji Validitas
Uji validitas yang digunakan adalah dengan metode korelasi Pearson, dengan menu Analyze >> Correlate >> Bivariate seperti pada gambar di bawah ini:
Gambar 1
Menu Korelasi Pearson
Setelah diklik pada menu Bivariate maka program SPSS akan mengarahkan ke box sebagai berikut:
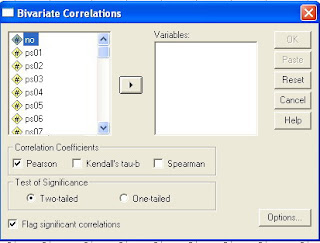
Gambar 2
Menu Box Bivariate Correlations
Di sebelah kiri merupakan indikator-indikator dari variabel penelitian, dan untuk menguji validitas pada indikator perilaku siswa, maka indikator ps01 sampai dengan ps14 dan Perilaku Siswa dipindah ke box sebelah kanan yang kosong sebagai berikut:
Gambar 3
Memasukkan Indikator
Setelah itu tekan OK di sebelah kanan atas pada box, sehingga program akan menghitung nilai R Pearson pada masing-masing indikator dengan nilai Skor total yaitu pada variabel Perilaku Siswa. Nilai yang dipergunakan untuk menguji validitas indikator adalah pada kolom paling kanan, sehingga akan ditampilkan sebagai berikut:
Tabel 1
Uji Validitas Indikator Perilaku Siswa
Perilaku Siswa | ||
PS01 | Pearson Correlation | .642(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS02 | Pearson Correlation | .655(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS03 | Pearson Correlation | .581(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS04 | Pearson Correlation | .633(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS05 | Pearson Correlation | .634(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS06 | Pearson Correlation | .772(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS07 | Pearson Correlation | .698(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS08 | Pearson Correlation | .755(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS09 | Pearson Correlation | .717(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS10 | Pearson Correlation | .802(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS11 | Pearson Correlation | .784(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS12 | Pearson Correlation | .741(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS13 | Pearson Correlation | .689(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
PS14 | Pearson Correlation | .695(**) |
Sig. (2-tailed) | .000 | |
N | 72 | |
Perilaku Siswa | Pearson Correlation | 1 |
Sig. (2-tailed) | . | |
N | 72 |
** Correlation is significant at the 0.01 level (2-tailed).
Interpretasi dapat dilakukan dengan 3 cara yaitu sebagai berikut:
1. Menggunakan tanda flag (*) di mana tanda satu buah flag (*) menunjukkan bahwa indikator tersebut signifikan pada taraf 5% dan tanda dua buah flag (**) menunjukkan bahwa indikator tersebut valid pada taraf 1%.
2. Menggunakan signifikansi pada baris kedua masing-masing indikator di mana indikator dinyatakan valid pada taraf 5% jika mempunyai signifikansi di bawah 0,05 dan valid pada taraf 1% jika mempunyai signifikansi di bawah 0,01.
3. Menggunakan R tabel, yaitu membandingkan nilai Pearson Correlation (baris pertama masing-masing indikator) dengan nilai R yang terdapat pada Tabel, di mana nilai R untuk sampel sebanyak 72 pada taraf 5% adalah sebesar 0,230.
Dengan demikian tampak bahwa semua indikator yang dipergunakan untuk mengukur variabel perilaku siswa adalah valid karena semua indikator terdapat tanda flag dua buah, dan signifikansi di bawah 0,05 semua. Selain itu, nilai Pearson Correlation semuanya juga di atas nilai R tabel yaitu sebesar 0,230.
2. Uji Reliabilitas
Uji reliabilitas menggunakan metode split half yaitu dengan memilih Analyze >> Scale >> Reliabilty yaitu sebagai berikut:
Gambar 5
Menu Uji Reliabilitas
Setelah diklik pada menu Reliability Analysis, maka program akan mengarahkan ke menu box sebagai berikut:
Gambar 6
Menu Box Reliabilitas
Pindahkan indikator ps01 sampai dengan ps14 dari kotak kiri ke kotak kosong di sebelah kanan dan pada Model di kiri bawah pilih menu Split half, yaitu sebagai berikut:
Gambar 7
Memasukkan Indikator
Setelah itu tekan OK, sehingga program akan menghitung dan mengeluarkan output sebagai berikut:
Gambar 8
Output Uji Reliabilitas Perilaku Siswa
Tampak bahwa terdapat N of cases yaitu jumlah sampel sebanyak 72 dengan indikator N of Items sebanyak 14. Korelasi antara part 1 dengan part 2 adalah sebesar 0,7032 dan Guttman Split Half adalah sebesar 0,8160 yang berada di atas nilai R tabel untuk 72 sampel yaitu sebanyak 0,230. Dengan demikian dinyatakan bahwa rangkaian kuesioner yang dipergunakan pada variabel perilaku siswa adalah reliabel.